Wintersportlerinnen und Wintersportler, die sich in verschneiten Gebirgsregionen bewegen, kennen die Warnzeichen für eine instabile Schneedecke: Wumm-Geräusche, Fernauslösungen und sich von selbst lösende Schneebretter. Dennoch hat sich unser Verständnis dafür, wie ein Skifahrer eine Schneebrettlawine auslösen kann, erst in den letzten Jahren verbessert.

Dies liegt nicht zuletzt daran, dass wir begonnen haben, die Bruchvorgänge innerhalb der Schneedecke als bruchmechanisches Problem aufzufassen. Die Kombination einer Schwachschicht und eines darüber liegenden, hinreichend verbundenen Schneebretts gilt als Schlüsselfaktor für die am weitesten verbreitete Lawinenart – die Schneebrettlawine (vgl. bergundsteigen #97).

Brüche der Schwachschicht sind die häufigste Ursache von durch Wintersportler ausgelösten Schneebrettlawinen (vgl. bergundsteigen #98). Schwachschichten sind häufig besonders porös und zeichnen sich durch grobkörnige, kantige Schneekristalle aus (vgl. bergundsteigen #94). Das Schneebrett hingegen ist gebunden, dichter gepackt und steifer, aber in gewissem Maße elastisch verformbar (vgl. bergundsteigen #97).

Der Aufbau der Schneedecke und die Lage einer möglichen Schwachschicht lassen sich anhand eines Schneeprofils ermitteln (vgl. bergundsteigen #98). Wie der Name sagt, ist die Schwachschicht die schwächste Schicht innerhalb der Schneedecke. Die Belastung durch einen Skifahrer kann dazu führen, dass die fragile Schwachschicht versagt und sich das Schneebrett oberhalb der Schwachschicht löst und ins Rutschen kommt.

Wie man an den geraden und markanten Anrisskanten von Schneebrettlawinen erkennen kann, ist das Versagen von Schneebrettern ein spröder Bruchprozess. Das gilt im Besonderen für das Versagen der fragilen Schwachschicht. Bruchvorgänge wie dieser innerhalb der Schneedecke spielen im Ingenieurwesen eine wichtige Rolle.

So fliegen Flugzeuge nur sicher, weil Ingenieurinnen und Ingenieure abschätzen können, wann Risse entstehen und ob diese unkontrolliert wachsen. Die Vorhersage von Rissentstehung ist auch im Ingenieurwesen herausfordernd. Dennoch stellt die Forschung Modelle bereit, die den physikalischen Versagensprozess beschreibbar und berechenbar machen.

Der geschichtete Schneedeckenaufbau und ein Kollaps anstelle klassischer Rissausbreitung machen Lawinenauslösung zu einem äußerst komplexen Vorgang. Trotzdem lassen sich bruchmechanische Modelle auf das Problem der Lawinenauslösung übertragen. Die Bruchmechanik ist so in der Lage, zur Bewertung der Lawinengefahr beizutragen.

Mit einem guten Verständnis des Versagensprozesses können geeignete Untersuchungsmethoden für Expertinnen und Experten der Lawinenwarndienste sowie Feldexperimente für Wintersportler entwickelt werden. Dennoch ist für die Gesamteinschätzung der Lawinensituation die Expertise verschiedener Disziplinen notwendig. Bruchmechanische Modelle benötigen beispielsweise Eingangsdaten der Meteorologie und ihre Ergebnisse müssen Anwendung in Strategiemethoden finden.

Antiriss, Wumm und Fernauslösung

Zur Weiterentwicklung unserer Vorstellung der Prozesse, die zum Auslösen einer Schneebrettlawine führen, haben in den letzten Jahrzehnten zahlreiche Studien, Experimente und theoretische Überlegungen (vgl. bergundsteigen #93) beigetragen. Dass nicht allein die Scherbelastung der Schneedecke für Lawinenauslösungen verantwortlich ist, wurde immer deutlicher.

Wumm-Geräusche und Fernauslösungen passen dazu nicht. Diese lassen sich erst mit Überlegungen zum Kollaps der Schwachschicht erklären. Abb. 1 zeigt ein viel beachtetes Foto einer Schwachschicht aus eingeschneitem Oberflächenreif und dem darüberliegenden Schneebrett. Die unterschiedliche Struktur ist hervorragend zu erkennen. In der linken Hälfte des Bilds ist die Schwachschicht gebrochen und kollabiert. Dies führte zum Durchriss des Schneebretts und ließ den rechten Teil der Schneedecke intakt.

Eine Modellvorstellung des Schwachschichtkollapses ist der Antiriss. Anti meint hierbei, dass bestehende Hohlstellen der porösen Schwachschicht durch ihren Kollaps verschwinden, anstatt dass sich neue Hohlstellen durch Rissöffnung bilden. Mathematisch und mechanisch gelten beim Riss und beim Antiriss die gleichen Gesetzmäßigkeiten – nur mit anderem Vorzeichen.

Mit dem Antiriss lässt sich die Zerstörung der Schwachschicht durch senkrecht zum Hang wirkende Kräfte und dadurch ihr Kollaps beschreiben. Ein von einem Skifahrer erzeugter lokaler Bruch kann sich aufgrund des Gewichts der Schneedecke weiträumig ausbreiten. Das plötzliche Setzen der Schneedecke ist mitunter sichtbar, spürbar und als Wumm bekannt.

Die Ausbreitung des Schwachschichtbruchs wird wie die Ausbreitung eines Risses beschrieben. So ist es möglich, dass sich ein im Flachen erzeugter Bruch bis in steile Hänge ausbreitet und sich dort ein Schneebrett löst. Obschon das Antiriss-Modell Wumm-Geräusch, Risse in der Schneedecke, Setzungsbewegungen sowie Fernauslösungen erklären kann, gibt es einige Kritik an seiner bisherigen mathematischen Formulierung.

In dieser ist ausschließlich die Deformation des Schneebretts berücksichtigt, Verformungen der Schwachschicht sind der Einfachheit halber ausgelassen. Dies führt zu einer falschen Berechnung der Deformationen der Schneedecke und lässt die lokale Belastung der Schwachschicht unberücksichtigt. Für die Bestimmung von Lasten, die zu einer Lawinenauslösung führen, muss im bisherigen Modell angenommen werden, dass es bereits gebrochene Zonen der Schwachschicht gibt.

Letztendlich bildet das Modell die Abhängigkeit von der Hangneigung nicht hinreichend ab. Die resultierende Frage ist nun, ob Scherung oder Kollaps der Schwachschicht für das Versagen der Schwachschicht maßgeblich sind. Legt man den aktuellen Stand der Forschung zur Tragfähigkeit von Bauwerken oder Maschinenkomponenten zugrunde, muss diese Frage mit „Beides zusammen!” beantwortet werden.

Wir haben dazu einige Überlegungen angestellt, moderne Ingenieurmethoden angewendet und so ein erweitertes Modell für Kollaps und Scherversagen der Schwachschicht entwickelt, das wir im Folgenden darlegen und zur Diskussion stellen wollen. Dieses Modell benötigt keine Annahmen über bereits vorhandene im Hang verteilte Defekte innerhalb der Schwachschicht.

Festigkeit und Bruchzähigkeit

Um beurteilen zu können, ob ein Material bricht, sind zwei Größen von zentraler Bedeutung: die beiden Materialeigenschaften Festigkeit und Bruchzähigkeit. Was zunächst ähnlich klingt, sind tatsächlich zwei vollkommen verschiedene und unabhängige Kenngrößen. Sie zeigen oftmals einen gegenläufigen Trend. Anschaulich lässt sich dies anhand von Kunststoffen erklären. Diese zeigen eine ausgesprochene Temperaturabhängigkeit:

❙ Die Bruchzähigkeit bestimmt, wie viel Kraft ich brauche, um einen Einschnitt (als Riss) in einer dünnen Kunststofffolie zum Wachsen zu bringen. Bei Raumtemperatur ist diese Kraft deutlich größer als wenn die Folie zuvor im Eisfach lag.

❙ Die Festigkeit erkenne ich hingegen daran, wie viel Kraft ich brauche, um eine Folie ohne Einschnitt zu zerreißen. Diese ist bei Raumtemperatur deutlich geringer als bei großer Kälte.

Steigt einer der beiden Werte, während der andere sinkt, ist offensichtlich, dass es sich um unabhängige Eigenschaften handelt. Im technischen Sinne bezeichnet man Festigkeit als die maximale Kraft, die ein Material auf einer bestimmten Querschnittsfläche übertragen kann, bevor das Material versagt.

Wenn allerdings örtlich sehr konzentrierte Belastungen, etwa in einer technischen Struktur an einer scharfen Kerbe (wie eine in Holz geschnitzte Kerbe) oder eben in der Schwachschicht direkt unter dem Skifahrer vorliegen, dann genügt diese Materialeigenschaft nicht, um Versagen zu beschreiben. Um beurteilen zu können, ob ein Riss entsteht und wächst, ist zusätzlich die Bruchzähigkeit entscheidend. Die Bruchzähigkeit ist die Energie, die beim Wachsen eines Risses für den Bruchprozess benötigt wird.

Diese Energie besteht aus vielen Anteilen, zum Beispiel der Oberflächenenergie neuer Oberflächen, der Energie für mikroskopische, bleibende Dehnung oder auch der Energieverlust durch örtliche Reibung. Daher muss berechnet werden, um welches Maß die elastisch gespeicherte Energie eines Systems abnimmt, wenn ein Riss länger wird. Diese freisetzbare Energie, die von der Gestalt der Struktur, der Risslänge und der Belastung abhängt, muss die Bruchzähigkeit übersteigen, damit ein Riss wachsen kann.

Diese Energiebedingung wird als Griffithsches Bruchkriterium bezeichnet und ist die Grundlage aller bruchmechanischen Analysen. Wie die Festigkeit ist die Bruchzähigkeit eine grundlegende charakteristische Eigenschaft eines Werkstoffes. Für die Analyse des Versagens der Schwachschicht benötigen wir also beide Materialkennwerte.

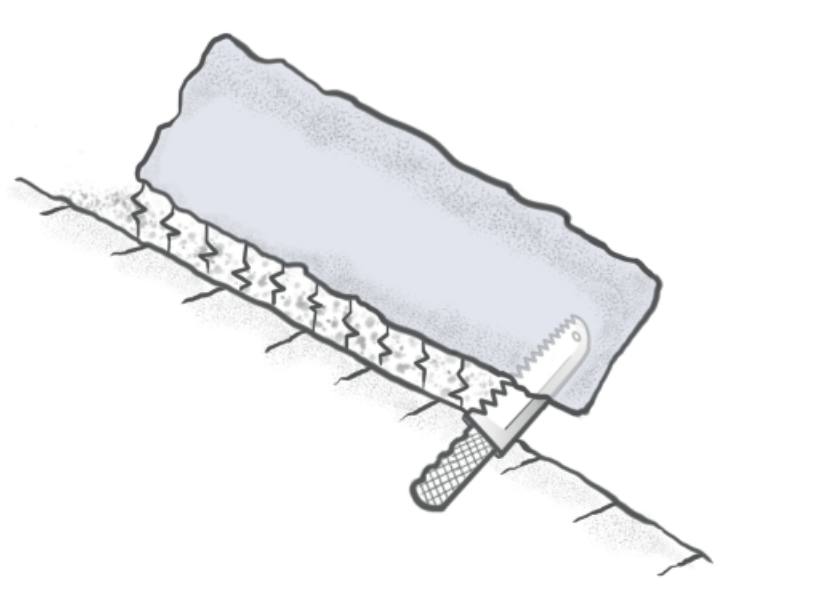
Und tatsächlich wurde für die Bestimmung der Bruchzähigkeit von Schwachschichten bereits in den frühen 2000ern ein Feldexperiment vorgeschlagen und etabliert. Mit dem Propagation Saw Test (PST, Abb. 2) wird genau diese kritische Energiefreisetzung bestimmt, indem bei konstanter Last die Risslänge verändert wird. Es wird dann notiert, ab wann plötzliche Rissausbreitung in der Schwachschicht stattfindet. Aus dieser Risslänge kann dann die Bruchzähigkeit rückgerechnet werden.

Tatsächlich entspricht der PST ziemlich genau den in der Bruchmechanik etablierten Laborversuchen zur Bestimmung der Bruchzähigkeit. Durch die gezielte Einbringung eines Risses spielt nur noch die Energiefreisetzung eine Rolle und der Einfluss der Festigkeit verschwindet. Einziger Unterschied ist, dass anstelle von typischerweise zugbelasteten Rissen im PST nun das Kollabieren einer Schwachschicht betrachtet wird. Es gelten jedoch die gleichen Gesetzmäßigkeiten und Modelle. Dies wurde bereits im AntirissModell ausgenutzt.

Schneedecke modellieren

Um das Verhalten der Schneedecke und die Bedingungen für das Auslösen einer Schneebrettlawine untersuchen zu können, benötigen wir zunächst ein vereinfachtes Modell. Dieses Modell besteht aus klassischen Elementen der technischen Mechanik und erlaubt eine mathematische Beschreibung der Zustände innerhalb der belasteten Schneedecke.

Dabei folgen wir dem Prinzip, mit einem möglichst einfachen Modell zu beginnen und nicht alle denkbaren Effekte, sondern nur die wesentlichsten zu berücksichtigen. Im Modell wird die Schneedecke als erweitertes Balkenelement dargestellt, das in der Lage ist, die Deformationen der Schneedecke infolge von Eigengewicht und Skifahrerlast zu beschreiben. Da die Schwachschicht eine entscheidende Rolle spielt, ist diese im Modell ebenfalls berücksichtigt.

Sie wird als nachgiebige Bettung, auf welcher der Balken ruht, modelliert, siehe Abb. 3. Damit ist es möglich, geschlossen-analytische Gleichungen für Deformationen und örtliche Belastungen zu erhalten. Die zusätzliche Berücksichtigung der Schwachschicht ist ein entscheidender Unterschied gegenüber bisherigen Modellen wie dem Antiriss-Modell. Sie erhöht die Komplexität der zu lösenden Gleichungen, erlaubt jedoch eine sehr gute Beschreibung der örtlichen Belastungen innerhalb der Schneedecke, sowohl senkrecht zum Hang (Druckbelastung) als auch die tangentiale Belastung parallel zum Untergrund (Scherbelastung).

Wie zuvor beschrieben ist es zusätzlich entscheidend berechnen zu können, wie viel Energie für einen Bruchprozess zur Verfügung steht. Dazu kann in diesem Modell eine Unterbrechung der Schwachschicht, also ein kollabierter Bereich, modelliert werden. Daraus kann dann die Änderung der gespeicherten Energie bei Veränderung der Größe des kollabierten Bereichs berechnet werden.

Für die Auslösung des Bruchvorgangs ist weder allein die Druckbelastung noch allein die Scherbelastung verantwortlich. Die Reihe eines Kartenhauses lässt sich schwerer umstoßen, wenn darauf ein schweres Buch liegt. Dies ist ein Beispiel dafür, wie eine Druckbelastung die Scherbelastbarkeit einer Struktur erhöhen kann. Die gegenseitige Beeinflussung verschiedener Belastungsarten wird als Interaktionsgesetz bezeichnet.

Es gilt sowohl für die örtliche Belastung als auch für die Energie. Der gewählte Modellierungsansatz liefert geschlossen-analytische Ausdrücke, das heißt Gleichungen, die sich auf einem Blatt Papier lösen ließen. Liegen die nötigen Eingangsgrößen wie die Eigenschaften von Schneebrett und Schwachschicht vor, lassen sich mit Computern (oder Smartphones) in Sekundenschnelle Lösungen berechnen.

Wie startet der Kollaps?

Die Vorhersage der Entstehung des ersten Risses in einer Struktur (dem Anriss) ist eine der herausforderndsten Aufgaben der Bruchmechanik. Festigkeit und Bruchzähigkeit reichen jeweils alleine nicht aus, um Rissentstehungen vollständig zu beschreiben. Für die Bildung von Rissen müssen beide Materialparameter zusammen berücksichtigt werden.

Zusammen mit dem Eigengewicht des Schneebretts erzeugt die Last eines Skifahrers örtliche Belastungen in der Schwachschicht. Abb. 4 zeigt, wie sich die örtlichen Belastungen unter Skifahrerinnen und Skifahrern konzentrieren. Wie zuvor beschrieben, muss zur Entstehung eines Risses genügend Energie für den Bruchprozess zur Verfügung stehen.

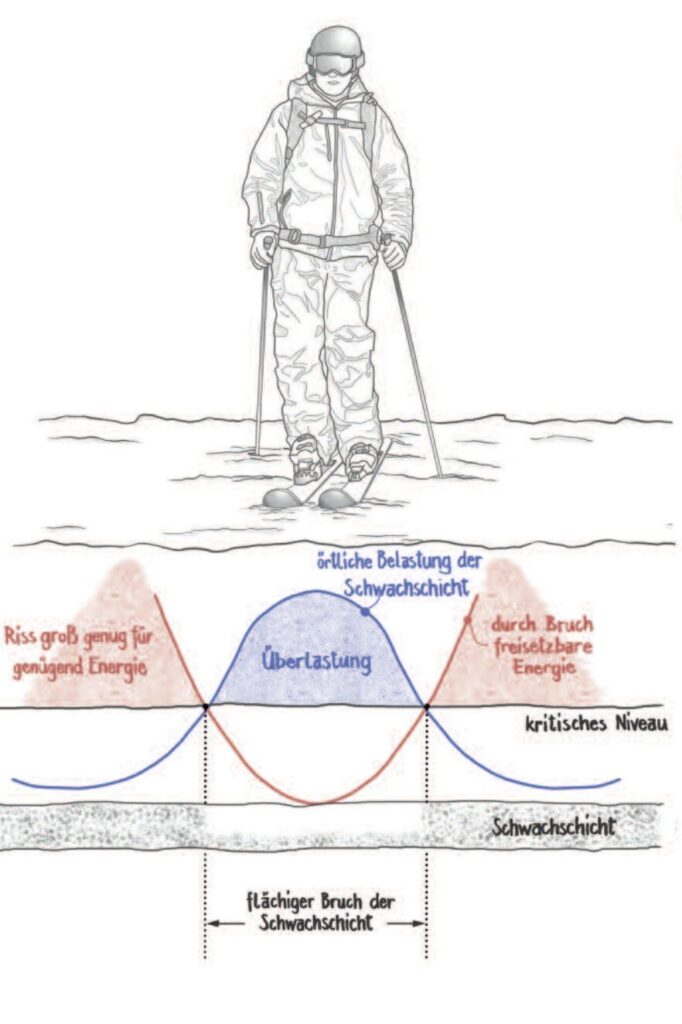
Längere Risse bedingen dabei eine stärkere Veränderung der Struktur und setzen daher mehr Energie frei. Betrachten wir die örtlichen Belastungen, wird die Festigkeit der Schwachschicht zuerst in einem kleinen Bereich unter dem Skifahrer überschritten, in dem die Belastungen konzentriert sind. Hier erwarten wir das Versagen der Schwachschicht. Damit die Schwachschicht kollabieren kann, muss jedoch zusätzlich ein Mindestmaß an Energie für den Bruchprozess zur Verfügung stehen.

Dies erfordert eine gewisse Mindestgröße des überlasteten Bereichs, wie in Abb. 4 dargestellt. Sind nur in einem kleinen Bereich unter dem Skifahrer die örtlichen Belastungen größer als die Festigkeit, wird dies nicht zu einem Anriss führen, weil schlichtweg nicht genug Energie für den dafür notwendigen Bruchprozess zur Verfügung steht. Dieser Fall ist in Abb. 5 dargestellt. Das heißt, die Bedingungen für örtliche Überlastung (der Festigkeit) und die hinreichende Energiefreisetzung für den Bruchprozess (die Bruchzähigkeit) sind hier direkt verknüpft.

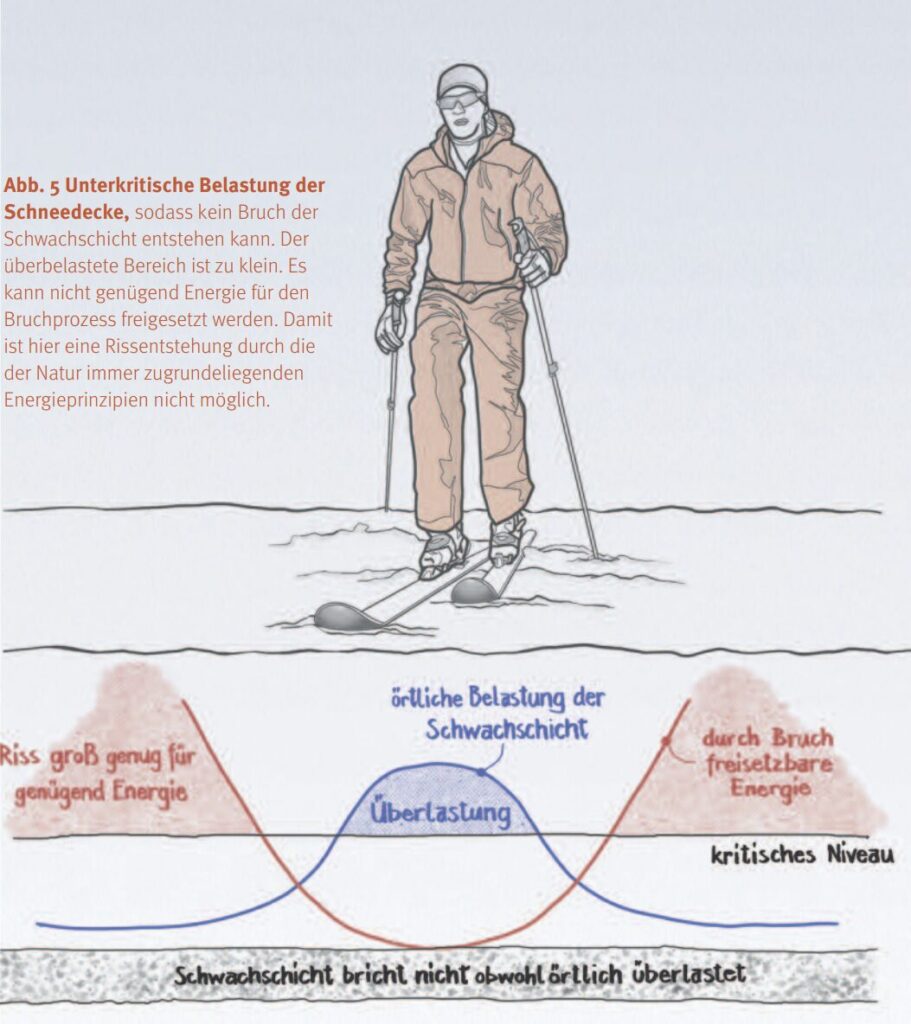
Verwendet man den zuvor dargestellten Modellierungsansatz, kann dieses sogenannte gekoppelte Kriterium für den initialen Kollaps mathematisch ausgewertet werden. Dann erhält man die kritische Zusatzbelastung, die zu einem Kollaps der Schwachschicht führt. Vergleicht man die mögliche Belastung durch eine Skifahrerin oder einen Skifahrer (Aufstieg, Abfahrt, Kurzschwung oder Sturz) mit diesem kritischen Wert, liefert dies eine Aussage, ob ein Bruch der Schwachschicht möglich ist.

Die Kopplung von Überlastung und Energie als gemeinsame Bedingung für Rissentstehung ist eine sehr wichtige Erkenntnis der modernen Bruchmechanikforschung. Die Übertragung dieses neuen Verständnisses auf den Bruchprozess innerhalb der Schneedecke bildet den Kern des hier vorgestellten Modells.

Dazu ist es zwingend notwendig, die Schwachschicht in der mathematisch-mechanischen Beschreibung der Schneedecke zu berücksichtigen. Die zweite Frage, die sich stellt, ist, ob sich ein initialer Kollaps allein durch das Gewicht der Schneedecke weiter ausbreitet. Auch diese Frage lässt sich mit Hilfe des gekoppelten Spannungs- und Energiekriteriums beantworten.

Ist bereits ein Riss vorhanden, liegt ein Sonderfall vor. In diesem Sonderfall spielt die Festigkeit keine Rolle mehr und die alleinige Bedingung für Rissfortschritt ist das zuvor genannte Griffithsche Kriterium. Es muss also die Änderung der gespeicherten Energie bei Fortschreiten des Risses berechnet werden. Dazu kann das entwickelte Modell der Schneedecke ebenfalls verwendet werden.

Sind die Risse besonders lang, muss allerdings zusätzlich berücksichtigt werden, dass die Schneedecke sich im Bereich der kollabierten Schwachschicht soweit durchbiegen kann, dass sie wieder aufliegt und Kräfte übertragen kann. Die Bedingung für den Rissfortschritt kann dann im Umkreis des Auslösepunktes ausgewertet werden.

In Abhängigkeit von der Hangneigung und der Dicke der Schneedecke kann sich der Kollaps dann weit oder weniger weit ausbreiten. Die Ausbreitung solcher Antirisse (Kollaps der Schwachschicht) wurde schon wissenschaftlich untersucht und in Feldexperimenten gemessen. Die Geschwindigkeiten liegen teilweise über 100 km/h und erklären so das großflächige Wumm-Geräusch und auch die nahezu unverzögerte Fernauslösung.

Ob das Schneebrett nun zuletzt nur großflächig absackt oder abreißt und den Hang hinunterrutscht, hängt von der Reibung und Festigkeit der Schneedecke ab. Dies ist nicht Schwerpunkt des hier beschriebenen Modells, aber ebenfalls berechenbar.

Erkenntnisse

In Abb. 6 und Abb. 7 sind Ergebnisse einer Auswertung unseres Modells dargestellt. Dabei wurden typische Werte einer Schneedecke als Eingangsparameter verwendet, um die auf die Schneedecke wirkende Kraft, die zur Auslösung führt, für unterschiedliche Hangneigungen zu berechnen. Es wurde dabei eine Schwachschicht aus Tiefenreif in 60 cm Tiefe betrachtet.

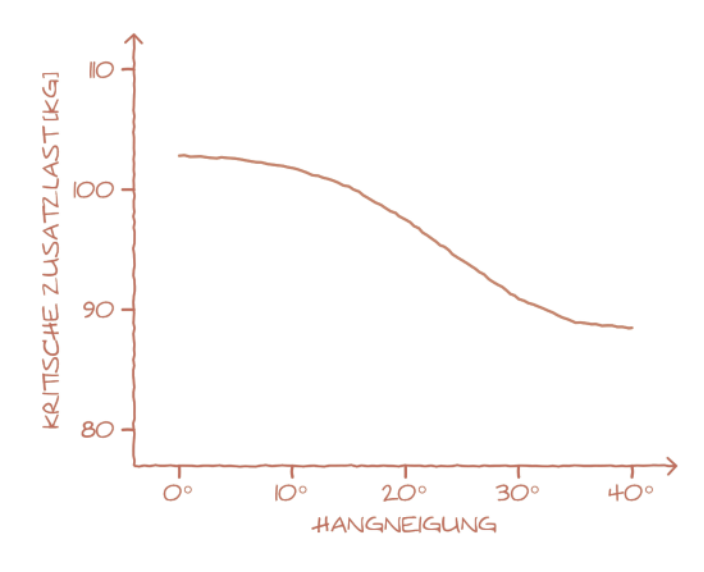
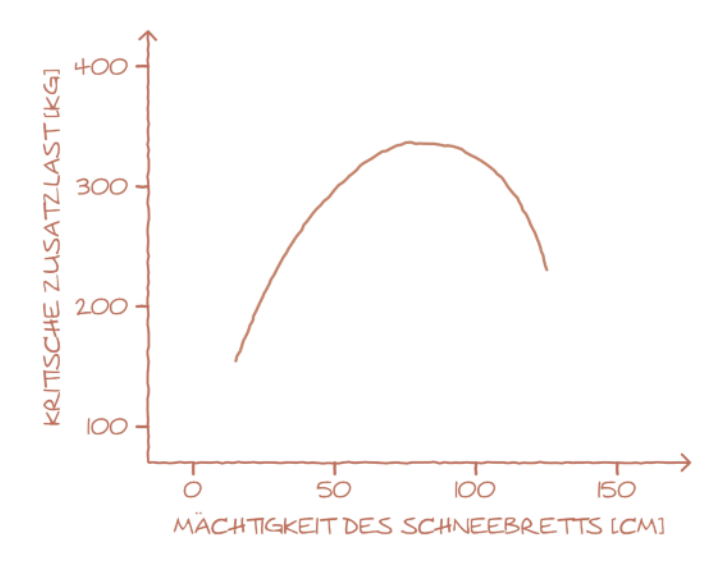
Die kritische Belastung, die zur Auslösung führt, liegt im Bereich der Belastung, die ein Skifahrer auf die Schneedecke ausübt. Die Belastbarkeit nimmt mit zunehmender Hangneigung deutlich ab (Abb. 6). Ändert man in dieser Betrachtung die Dicke der Schneedecke über der Schwachschicht, so ergibt sich ein Zusammenhang, wie er in Abb. 7 dargestellt ist.

Eine dickere Schneedecke verteilt die Zusatzlast durch die Skifahrerin oder den Skifahrer gleichmäßiger und sowohl die örtliche Belastung als auch die für den Bruchprozess zur Verfügung stehende Energie nimmt ab. Dies geschieht in erster Linie durch die zunehmende Biegesteifigkeit des Schneebretts. Dadurch ergibt sich zunächst mit steigender Dicke eine zunehmende Belastbarkeit, also eine höhere kritische Zusatzlast durch eine Skifahrerin oder einen Skifahrer.

Wird die Schneedecke jedoch noch dicker, spielt das Eigengewicht der Schneedecke eine immer größere Rolle. Dann sind zunehmend kleinere Zusatzlasten durch eine Skifahrerin oder einen Skifahrer bereits kritisch und führen in Kombination mit dem Eigengewicht zu einem Kollaps der Schwachschicht. Das Modell kann auch dazu benutzt werden, den oben beschriebenen Propagation Saw Tests (PST) vorteilhaft physikalisch auszuwerten (Abb. 2).

Aus der im Versuch bestimmten kritischen Risslänge, die zum plötzlichen Kollaps der Schwachschicht führt, lässt sich die Bruchzähigkeit der Schwachschicht ermitteln. Auf dem International Snow Science Workshop 2018 wurden von anderen Teilnehmern neue Formen des PST-Versuchs mit leicht geänderter Belastung vorgestellt und diskutiert. Mit diesem Modell ist es nun möglich, solche Experimente im bruchmechanischen Sinne auszuwerten und den tatsächlichen Abhängigkeiten der Versagensparameter der Schwachschicht nachzuspüren.

Referenzen und Vertiefungsmaterial

• Gaume, J., Gast, T., Teran, J., van Herwijnen, A., Jiang, C. (2018). Dynamic anticrack propagation in snow. Nature communications, 9(1), Artikelnummer 3047.
• Gaume, J., van Herwijnen, J., Chambon, G., Wever, N., Schweizer, J. (2016). Snow fracture in relation to slab avalanche release: critical state for the onset of crack propagation. The Cryosphere 11, Seiten 217–228.
• Gauthier, D., Jamieson, B. (2006). Towards a field test for fracture propagation propensity in weak snowpack layers. Journal of Glaciology, 52(176), Seiten 164–168.
• Gross, D., Seelig, T. (2016). Bruchmechanik: mit einer Einführung in die Mikromechanik. Springer-Verlag, Heidelberg, 349 Seiten.
• Harvey, S., Rhyner, H., Schweizer, J. (2012). Lawinenkunde. Bruckmann Verlag GmbH, München, 192 Seiten.
• Heierli, J., van Herwijnen, A., Gumbsch, P., Zaiser, M. (2008): Anticracks: A new Theory of Fracture Initiation and Fracture Propagation in Snow. In: Proceedings of the International Snow Science Workshop ISSW 2008. Whistler, Kanada, Seiten 9–15.
• Höller, P. (2016). Schneewissen einst&heute. bergundsteigen #96. Österreichischer Alpenverein, Innsbruck, 25(3), Seiten 80–87.
• Mitterer, C., Reuter, B., Proksch, M., Schweizer, J. (2016). Das Schneeprofil. bergundsteigen #97. Österreichischer Alpenverein, Innsbruck, 25(4), Seiten 44–49.
• Reiweger, I., Gaume, J., Schweizer, J. (2015). A new mixed-mode failure criterion for weak snowpack layers. Geophysical Research Letters, 42(5), Seiten 1427–1432.
• Reuter, B., Schweizer, J., van Herwijnen, A. (2015). A process-based approach to estimate point snow instability. Cryosphere, 9(3), Seiten 837–847.
• Rosendahl, P.L., Lübke, V., Weißgraeber, P. (2018). Anticrack nucleation in snowpacks without assuming initial defects: modeling dry snow slab avalanches. In: Proceedings of the International Snow Science Workshop ISSW 2018. Innsbruck, Österreich, Seiten. 880–884.
• Schweizer, J., Jamieson, J. B., Schneebeli, M. (2003). Snow avalanche formation. Reviews of Geophysics, 41(4), Artikelnummer 1016.
• Schweizer, J. und Reuter, B. (2015). Lawinenbildung. bergundsteigen #93. Österreichischer Alpenverein, Innsbruck, 24(4), Seiten 43–53.
• Schweizer, J., Reuter, B., van Herwijnen, A., Gaume, J. (2016). Avalanche Release 101. In: Proceedings of the International Snow Science Workshop ISSW 2016. Breckenridge, Colorado, Seiten 1–11.
• Sigrist, C., Schweizer, J. (2007). Critical energy release rates of weak snowpack layers determined in field experiments. Geophysical Research Letters, 34(3), Artikelnummer L03502.
• Techel, F., Winkler, K. (2015). Fürchtet den Altschnee. bergundsteigen #90. Österreichischer Alpenverein, Innsbruck, 24(1), Seiten 34–40.
• van Herwijnen, A., Jamieson, B. (2005). High-speed photography of fractures in weak snowpack layers. Cold Regions Science and Technology, 43(1–2), Seiten 71–82.
• Weißgraeber, P., Leguillon, D., Becker, W. (2016). A review of Finite Fracture Mechanics: crack initiation at singular and non-singular stress raisers. Archive of Applied Mechanics, 86(1–2), Seiten 375–401.
• Würtl, W., Riedl, H. (2017). Schneedeckenanalyse für Praktiker. bergundsteigen #98. Österreichischer Alpenverein, Innsbruck, 26(1), Seiten 56–61.